ALGORITMA DAN PEMOGRAMAN2

SORTING (PENGURUTAN)

Pengertian Sorting

Pengurutan data dalam struktur data sangat penting terutama untuk data yang beripe data numerik ataupun karakter. Pengurutan dapat dilakukan secara ascending (urut naik) dan descending (urut turun). Pengurutan (Sorting) adalah proses pengurutan data yang sebelumnya disusun secara acak sehingga tersusun secara teratur menurut aturan tertentu.

Contoh:

Data Acak :

5 6 8 1 3 25 10

Ascending : 1 3 5 6 8 10 25

Descending : 25 10 8 6 5 3 1

Deklarasi Array Sorting

Mendeklarasikan array secara global:

int data[100];

int n; //untuk jumlah data

Fungsi Tukar 2 Buah Data:

void tukar(int a,int b)

{

int tmp;

tmp = data[a];

data[a] = data[b];

data[b] = tmp;

}

Sorting merupakan suatu proses untuk menyusun kembali himpunan obyek menggunakan aturan tertentu. Sorting disebut juga sebagai suatu algoritma untuk meletakkan kumpulan elemen data kedalam urutan tertentu berdasarkan satu atau beberapa kunci dalam tiap-tiap elemen.

Pada dasarnya ada dua macam urutan yang biasa digunakan dalam suatu proses sorting:

1. Urut naik (ascending) Mengurutkan dari data yang mempunyai nilai paling kecil sampai paling besar.

2. Urut turun (descending) Mengurutkan dari data yang mempunyai nilai paling besar sampai paling kecil.

Mengapa harus melakukan sorting data?

Ada banyak alasan dan keuntungan dengan mengurutkan data. Data yang terurut mudah untuk dicari, mudah untuk diperiksa, dan mudah untuk dibetulkan jika terdapat kesalahan. Data yang terurut dengan baik juga mudah untuk dihapus jika sewaktu-waktu data tersebut tidak diperlukan lagi. Selain itu, dengan mengurutkan data maka kita semakin mudah untuk menyisipkan data atapun melakukan penggabungan data.

Jenis-Jenis Pengurutan:

1. Bubble sort (sederhana tetapi lambat)

Pengertian Bubble Sort

Bubble Sort (metode gelembung) adalah metode pengurutan dengan cara melakukan penukaran data dengan tepat disebelahnya secara terus menerus sampai bisa dipastikan dalam satu iterasi tertentu tidak ada lagi perubahan. Jika tidak ada perubahan berarti data sudah terurut. Disebut pengurutan gelembung karena masing-masing kunci akan dengan lambat menggelembung ke posisinya yang tepat.

Kelebihan dan Kekurangan Bubble Sort

- Kelebihan :

1. Metode Bubble Sort merupakan yang paling simple

2. Metode Bubble Sort muda di pahami algoritmanya

- Kelemahan :

Meskipun simpel metode Bubble Sort merupakan metode pengurutan yang paling tidak efisien. Kelemahan BubbleSort adalah pada saat mengurutkan data yang sangat besar akan mengalami kelambatan luar biasa, atau dengan kata lain kinerja memburuk cukup signifikan ketika data yang diolah jika data cukup banyak. Kelemahan lain adalah jumlah pengulangan akan tetap sama jumlahnya walaupun data sesungguhnya sudah cukup terurut. Hal ini disebabkan setiap data dibandingkan dengan setiap data yang lain untuk menentukan posisinya.

Algoritma dari Bubble Sort

- Membandingkan data ke-i dengan data ke-(i+1) (tepat bersebelahan). Jika tidak sesuai maka tukar (data ke-i = data ke-(i+1) dan data ke-(i+1) = data ke-i). Apa maksudnya tidak sesuai? Jika kita menginginkan algoritme menghasilkan data dengan urutan ascending (A-Z) kondisi tidak sesuai adalah data ke-i > data ke-i+1, dan sebaliknya untuk urutan descending (A-Z).

- Membandingkan data ke-(i+1) dengan data ke-(i+2). Kita melakukan pembandingan ini sampai data terakhir. Contoh: 1 dgn 2; 2 dgn 3; 3 dgn 4; 4 dgn 5 … ; n-1 dgn n.

- Selesai satu iterasi, adalah jika kita sudah selesai membandingkan antara (n-1) dengan n. Setelah selesai satu iterasi kita lanjutkan lagi iterasi berikutnya sesuai dengan aturan ke-1. mulai dari data ke-1 dgn data ke-2, dan seterusnya.

- Proses akan berhenti jika tidak ada pertukaran dalam satu iterasi.

Program Bubble Sort

#include <stdio.h>

#define N 20

int bubble(int n);

int i,j,A[N];

main()

{

int jml;

printf("\t METODE BUBBLE SORT \n\n");

printf("Masukkan jumlah bilangan: ");

scanf("%d",&jml);

printf("\n");

// input data

for (i=0;i<jml;i++)

{

printf("Bilangan ke %d : ",i+1);

scanf("%d",&A[i]);

}

printf("\n");

// mengurutkan data

bubble(jml);

// menampilkan data

printf("Data yang sudah terurut : \n");

for (i=0;i<jml;i++)

{

printf("%d\n",A[i]);

}

// fungsi bubble

int bubble(int n)

{

int temp;

for (i=1;i<=n-1;i++)

{

for (j=i;j<n;j++)

{

if (A[i-1]>A[j])

{

temp = A[i-1];

A[i-1] = A[j];

A[j] = temp;

}

OUTPUTNYA

Contoh Program Bubble Sort

OUTPUTNYA

2. Quick sort (cepat tetapi rumit)

Quick Sort merupakan salah satu algoritma pengurutan data yang menggunakan teknik membagi data menjadi partisi-partisi. metode quick sort disebut juga dengan nama partition exchange sort.

Untuk memulai proses pengurutan, pertama-tama sebuah data dipilih dari kelompok data sebagai data pivot. Posisi data pivot dapat dicari dengan menggunakan rumus :

i = (indeks awal + indeks akhir) div 2

Kemudian elemen-elemen data akan diatur, sehingga nilai data pivot yang terletak di posisi ke I memenuhi kondisi sebagai berikut :

Semua data di posisi ke 1 sampai dengan ke I-1 lebih kecil atau sama dengan pivot atau data[i]<=pivot.
Semua data di posisi ke I+1 sampai dengan ke N lebih besar atau sama dengan pivot atau data[i]>=pivot.

Contoh :

Ada 12 data sebagai berikut :

indeks 1 2 3 4 5 6 7 8 9 10 11 12

Data 33 99 18 7 5 45 57 25 55 10 40 50

Pos = (1+12) div 2 = 6

Pivot = data[ pos] = 45

Data 45 terpilih sebagai data pivot. Setelah diatur, maka posisi urutan data sebagai berikut :

indeks 1 2 3 4 5 6 7 8 9 10 11 12

Data 33 25 18 7 5 10 40 45 55 50 57 99

Dimana :

Semua elemen di posisi ke 1 sampai dengan posisi ke 8 lebih kecil atau sama dengan nilai 45.
Semua elemen di posisi ke 9 lebih besar atau sama dengan 45.

Dengan demikian, data tersebut akan terpecah menjadi 2 partisi, satu partisi di sisi kiri 57 dan satu partisi di sisi kanan 57 sebagai berikut :

[33 25 18 7 5 10 40 ] 45 [55 50 57 99]

Dengan cara yang sama, proses partisi diulangi lagi untuk masing-masing partisi baik di sisi kanan maupun di sisi kanan. Jadi setiap partisi yang diperoleh akan dipartisi lagi hingga diperoleh hasil pengurutan data.

Dalam proses partisi dengan metode quick sort dapat selesaikan dengan menggunakan prosedur rekursi. Karena proses partisi dengan cara sama selalu diulangi. Proses partisi dibentuk dalam sebuah prosedur atau fungsi dan akan memanggil dirinya sendiri.

Contoh Program Quick Sort

#include<stdio.h>
void quicksort(int number[25],int first,int last){
int i, j, pivot, temp;
if(first<last){
pivot=first;
i=first;
j=last;
while(i<j){
while(number[i]<=number[pivot]&&i<last)
i++;
while(number[j]>number[pivot])
j--;
if(i<j){
temp=number[i];
number[i]=number[j];
number[j]=temp;
}
}
temp=number[pivot];
number[pivot]=number[j];
number[j]=temp;
quicksort(number,first,j-1);
quicksort(number,j+1,last);
}
}
int main(){
int i, count, number[25];
printf("Enter some elements (Max. - 25): ");
scanf("%d",&count);
printf("Enter %d elements: ", count);
for(i=0;i<count;i++)
scanf("%d",&number[i]);
quicksort(number,0,count-1);
printf("The Sorted Order is: ");
for(i=0;i<count;i++)
printf(" %d",number[i]);
return 0;
}
OUTPUTNYA

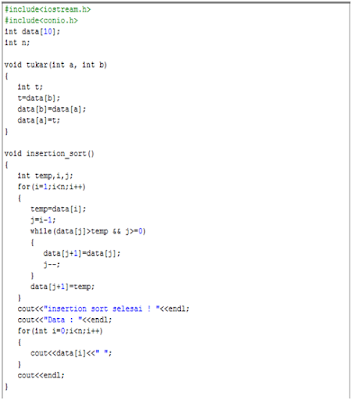
3. Insertion Sort

Cara kerja insertion sort sebagaimana namanya.Pertama-tama, dilakukan proses iterasi, dimana di setiap iterasi insertion sort memindahkan nilai elemen,kemudian menyisipkannya berulang-ulang sampai ketempat yang tepat. Begitu seterusnya dilakukan. Dari proses iterasi, seperti biasa, terbentuklah bagian yang telah di-sorting dan bagian yang belum.

Algoritma Insertion Sort. Algoritma Insertion Sort dapat dirangkum sebagai berikut:

1.) Simpan nilai Ti kedalam variabel sementara, dengan i = 1.

2.) Bandingkan nilainya dengan elemen sebelumnya.

3.) Jika elemen sebelumnya (Ti-1) lebih besar nilainya daripada Ti, maka tindih nilai Ti dengan nilai Ti-1 tersebut. Decrement i (kurangi nilainya dengan 1).

4.) Lakukan terus poin ke-tiga, sampai Ti-1 ≤ Ti.

5.)Jika Ti-1 ≤ Ti terpenuhi, tindih nilai di Ti dengan variabel sementara yang disimpan sebelumnya.

6.) Ulangi langkah dari poin 1 di atas dengan i di-increment (ditambah satu).

Contoh Program Insertion Sort

OUTPUTNYA

4.Merge sort

Metode pengurutan merge sort adalah metode pengurutan lanjut, sama dengan metode Quick Sort. Metode ini juga menggunakan konsep devide and conquer yang membagi data S dalam dua kelompok yaitu S1 dan S2 yang tidak beririsan (disjoint). Proses pembagian data dilakukan secara rekursif sampai data tidak dapat dibagi lagi atau dengan kata lain data dalam sub bagian menjadi tunggal.

Setelah data tidak dapat dibagi lagi, proses penggabungan (merging) dilakukan antara sub-sub bagian dengan memperhatikan urutan data yang diinginkan (ascending/kecil ke besar atau descending/besar ke kecil). Proses penggabungan ini dilakukan sampai semua data tergabung dan terurut sesuai urutan yang diiginkan. Kompleksitas algoritma merge sortadalah O(n log n).

Secara umum, algoritma merge sort dapat diimplementasikan secara rekursif. Fungsi rekursif adalah sebuah fungsi yang didalam implementasinya memanggil dirinya sendiri. Pemanggilan diri sendiri ini berakhir jika kondisi tertentu terpenuhi (terminated condition is true). Pada contoh berikut ini, terminated condition dari proses rekursif mergesort akan berakhir jika data tidak dapat dibagi lagi (data tunggal telah diperoleh). Dengan kata lain, proses pembagian data dilakukan terus selama S.size > 1 (belum tunggal).

Algoritma lain yang menggunakan Divide and Conquer dalam pengurutan adalah Merge Sort.

Secara konseptual, untuk sebuah array berukuran n,
Merge Sort bekerja sebagai berikut:
1. Jika bernilai 0 atau 1, maka array sudah terurut.

2. Jika Array tidak terurut, bagi menjadi 2 sub-array dengan ukuran n/2.

3. Urutkan setiap sub array. Jika sub array tidak cukup kecil lakukan langkah kedua dengan rekursif.

4. Menggabungkan sub array menjadi satu array.

Contoh penerapan atas sebuah larik/array dengan data yang akan diurutkan {6,3,5,1,8,2,4,7} ditunjukkan pada gambar 1. Pertama kali larik tersebut dibagi menjadi dua bagian, {6,3,5,1} dan {8,2,4,7}. Larik {6,3,5,1} dibagi menjadi dua bagian yaitu, {6,3} dan {5,1}. Larik {6,3} dibagi menjadi dua bagian yaitu, {6} dan {3}. Selanjutnya karena {6} dan {3} sudah tidak bisa dibagi lagi maka di merge dan diurutkan menjadi {3,6}. Larik {5,1} dibagi menjadi dua bagian yaitu, {5} dan {1}. Selanjutnya {5} dan {1} dilakukan merge dan diurutkan menjadi {1,5}. Larik {3,6} dan {1,5} dimerge dan diurutkan menjadi {1,3,5,6}. Larik {8,2,4,7} dibagi menjadi dua bagian yaitu, {8,2} dan {4,7}. Larik {8,2} dibagi menjadi dua bagian yaitu, {8} dan {2}. Selanjutnya {8} dan {2} di merge dan diurutkan menjadi {2,8}. Larik {4,7} dibagi menjadi dua bagian yaitu, {4} dan {7}. Selanjutnya {4} dan {7} dilakukan merge dan diurutkan menjadi {4,7}. Larik {2,8} dan {4,7} dimerge dan diurutkan menjadi {2,4,7,8}. Larik {1,3,5,6} dan larik {2,4,7,8} dimerge dan diurutkan menjadi {1,2,3,4,5,6,7,8}.

Merge sort adalah sort yang dilakukan dengan teknik merge (menggabungkan) dua buah array kedalam sebuah array yang baru. Algoritma merge sort membagi tabel menjadi dua tabel yang sama besar. Masing - masing tabel diurutkan secara rekursif, dan kemudian digabungkan kembali untuk membentuk tabel yang terurut.

Setelah data diurutkan kembali, maka tahap terakhir adalah data tersebut disatukan/dikombain.

Contoh Program Merge sort

#include <iostream>
using namespace std;
void merge(int low, int mid, int up);
void mergeSort(int low, int up);
int a[50];
int main()
{
int jumlahBil,i;
cout<<"Masukkan Jumlah element Array"<< endl;
cin>>jumlahBil;
for(int i=0; i<jumlahBil;i++)
{
cout<<"Bilangan ke-"<< i+1 << endl;
cin>>a[i];
}
mergeSort(1,jumlahBil);
for(i=1;i<=jumlahBil;i++)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}
void merge(int low, int mid, int up)
{
int h, i,j,k;
int b[50];
h = low;
i = low;
j = mid+1;
while((h<=mid)&&(j<=up))
{
if(a[h] < a[j])
{
b[i]=a[h];
h++;
}
else
{
b[i]=a[j];
j++;
}
i++;
}
if(h>mid)
{
for(k=j;k<=up;k++){
b[i]=a[k];
i++;
}
}
else
{
for(k=h;k<=mid;k++)
{
b[i]=a[k];
i++;
}
}
for(k=low;k<=up;k++) a[k]=b[k];
}
void mergeSort(int low, int up)
{

int mid;
if(low<up)
{
mid=(low+up)/2;
mergeSort(low,mid);
mergeSort(mid+1,up);
merge(low,mid,up);
}
}

OUTPUTNYA

5 Selection Sort

Algoritma sorting sederhana yang lain adalah Selection Sort. Ide dasarnya adalah melakukan beberapa kali pass untuk melakukan penyeleksian elemen struktur data. Untuk sorting ascending (menaik), elemen yang paling kecil di antara elemen-elemen yang belum urut, disimpan indeksnya,kemudian dilakukan pertukaran nilai elemen dengan indeks yang disimpan tersebut dengan elemen yang paling depan yang belum urut. Sebaliknya, untuk sorting descending (menurun), elemen yang paling besar yang disimpan indeksnya kemudian ditukar.

Algoritma Selection Sort Algoritma selection sort dapat dirangkum sebagai berikut:

1.) Temukan nilai yang paling minimum (atau sesuai keinginan) di dalam struktur data. Jika ascending, maka yang harus ditemukan adalah nilai yang paling minimum. Jika descending, maka temukan nilai yang paling maksimum.

2.) Tukar nilai tersebut dengan nilai pada posisi pertama di bagian struktur data yang belum diurutkan.

3.) Ulangi langkah di atas untuk bagian struktur data yang tersisa.